自発変化の方向を決定することができるヘルムホルツの自由エネルギーについてその定義とヘルムホルツの使える条件と自発変化の方向について本記事では解説します。
ヘルムホルツの自由エネルギーが生まれた経緯
前の記事で述べたように熱力学第二法則は以下のように表されました。\(\)
熱力学第二法則(エントロピー増大則)
任意の断熱過程に対して常に\(\Delta S\geq 0\)が成り立つ。
ゆえに熱の出入りがない孤立系にも適用することができ、孤立系の自発変化の方向は以下のようになります。
孤立系の自発方向の向き:\(\Delta S\gt 0\)
しかし自然界などにおいて孤立系となる場面はほとんどなく、たいていはある系は他の系(外界など)と熱の交換や仕事をしたりしています。
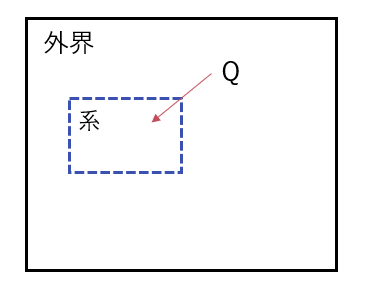
そうした場合においても自発変化の向きが分かるようになりたい。そうして生まれたのがヘルムホルツの自由エネルギーとギブスの自由エネルギーになります。
先に述べますが等温等積な系における自発変化の方向を表せるのがヘルムホルツの自由エネルギーで、等温等圧な系における自発変化の方向を表せるのがギブスの自由エネルギーです。
ではヘルムホルツの自由エネルギーについて詳しく見てみましょう。
ヘルムホルツの自由エネルギーの定義と自発変化の向き
ヘルムホルツの自由エネルギーは等温等積な系における自発変化の方向を表すものになります。

では系が熱量\(Q\)を受け取って等温等積で非可逆変化したときのエントロピー変化をみてみましょう。
系のエントロピー変化を\(\Delta S\)、外界のエントロピー変化を\(\Delta S_{sur}\)とします。
等積であるから仕事の変化\delta W=0かつ、外界から系に熱量が\(Q\)だけ移動してるから、
$$\Delta S_{sur}=\frac{-Q}{T_{sur}}=-\frac{\Delta U}{T_{sur}}\cdots①$$
外界と系あわせて全体的にみると孤立系であるから、全体の自発変化の向きは
$$\Delta S_{tot}\gt 0\cdots②$$
この式②を変形して外界に関する状態量を消して系のみの状態量で表すことができれば等温等積な系の自発変化の方向を系のみの情報から決定することができるようになります。
ゆえに式①より、
$$\begin{eqnarray}\Delta S_{tot} &=& \Delta S_{sur}+\Delta S \\ &=& -\frac{\Delta U}{T_{sur}}+\Delta S \gt 0 \end{eqnarray}$$
平衡状態において外界と系の温度が等しいから
$$\Delta(U-TS) \lt 0$$
よってヘルムホルツの自由エネルギー\(A\)を以下のように定義すると、
$$A=U-TS$$
等温等積な系における自発変化の向きは
$$\Delta A \lt 0$$
つまりヘルムホルツの自由エネルギーが減少する向きに進むことがわかります。
このようにして孤立系以外の系の自発変化の向きも熱力学第二法則を用いて決定することができるのです。
等温変化の最大仕事

左図の系が等温で変化するときを考えると、熱力学第二法則から準静的な過程も含め、
$$\Delta S_{tot}=\Delta S_{sur}+\Delta S\geq 0\cdots③$$
と表すことができる。
ここで系がされる仕事を\(W\)とすると、熱力学第一法則より
$$Q=\Delta U-W$$
ゆえに、
$$\Delta S_{sur}=-\frac{Q}{T}=-\frac{\Delta U-W}{T}$$
これを式③に代入すると、
$$-\frac{\Delta U-W}{T}+\Delta S$$
これを整理すると、
$$W\geq \Delta(U-TS)$$
つまり
$$-W\leq -\Delta A$$
が成り立ちます。
この式から等温変化における系がしうる最大の仕事が\(-\Delta A\)となり、それは準静的過程において達成されることが分かります。。
このようにヘルムホルツの自由エネルギーは等温過程と関係が深い状態量になるのです。
次の記事では等温等圧な系の自発変化の向きを定めるギブスの自由エネルギーについて解説するので興味のある方はそちらもあわせてご覧ください。



コメント