いままで学習した微分方程式は正規形、つまり微分方程式が\(y^(n)=f(x,y’,y”,…,y^(n-1))\)で表せるものであった。今回の記事では正規形でない微分方程式、非正規形1次微分方程式で一般解を導くことができる方程式の代表例であるクレローの微分方程式について、その形と解法について解説していく。
クレローの微分方程式
クレローの微分方程式とは以下の形の微分方程式のことを言う。\(\)
$$y=xy’+f(y’)\cdots①$$
この微分方程式の解は一般解の任意定数をどう変化させても現れない解がでてくいままでとは異なった面を持つ。ではクレローの微分方程式の解き方についてみていこう。
解法
\(y’=p\)と置き、①の両辺を\(x\)で微分すると
$$p=p+xp’+f'(p)p’$$
整理して、
$$(x+f'(p))p’=0$$が成り立つ。
ゆえに、
\(⑴p’=0\)または\(⑵x+f'(p)=0\)である。
⑴\(p’=0\)のとき、\(p=C\)(Cは任意定数)であるから、これを①に代入すると一般解
$$y=Cx+f(C)$$が得られる。
⑵\(x+f'(p)=0\cdots②\)のとき、式①と②から\(p\)を消去することで一般解では表すことのできない特異解を得ることができる。
では例題でこの解法を具体的に見てみよう。
練習問題
次のクレローの微分方程式を解け
$$⑴y=xy’-e^{y’}$$
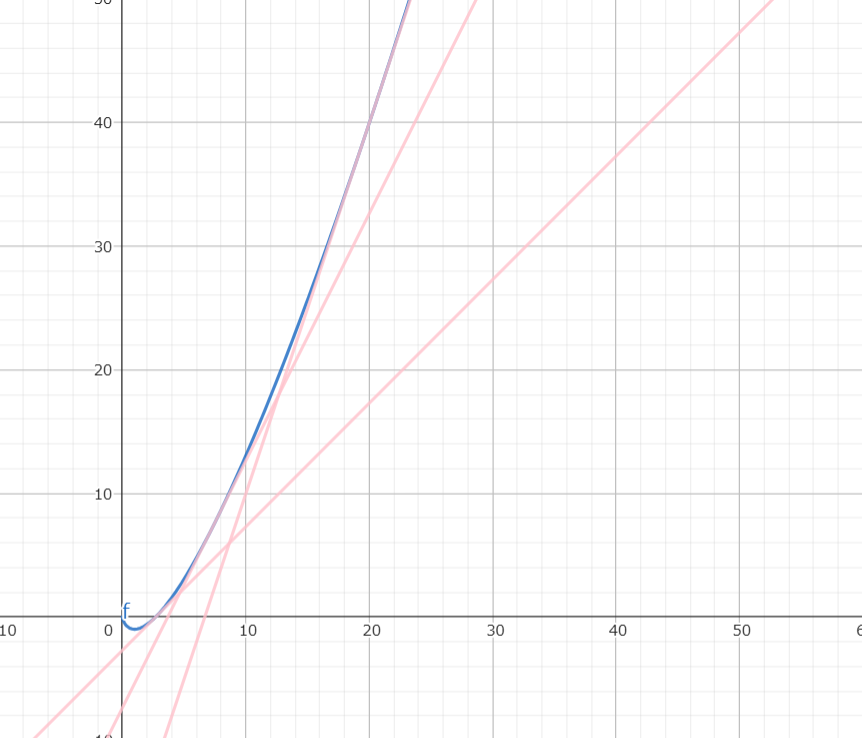
$$⑵y=xy’-{y’}^2$$
解答
⑴\(y’=p\)として問題文の両辺を\(x\)で微分すると、
$$p=p+xp’-e^pp’$$
$$(x-e^p)p’=0$$
\(p’=0\)のとき、\(p=C\)(Cは任意定数)であるから、これを問題文に代入して一般解
$$y=Cx-e^C$$が得られる。
\(x-e^p=0\)のとき、\(p=logx\)であるから、これを問題文に代入すると特異解
$$y=(logx-1)x$$が得られる。
解をグラフに示すと右図のようになる。
青線が特異解であり、赤色がC=1,C=2,C=3のときの一般解の曲線群である。
青線は赤色の曲線群に各点で接しており、青線は包括線と呼ばれる。
⑵\(y’=p\)として問題文の両辺を\(x\)で微分すると、
$$p=p+xp’-2pp’$$
$$(x-2p)p’=0$$
\(p’=0\)のとき、\(p=C\)(Cは任意定数)であるから、これを問題文に代入して一般解
$$y=Cx-C^2$$が得られる。
\(x-2p=0\)のとき、\(p=\frac{1}{2}x\)であるから、これを問題文に代入すると特異解
$$y=\frac{1}{4}x^2$$が得られる。
前の記事
次の記事
コメント