\(x,y\)を独立変数としたときの\(u(x,y)\)に関するラグランジュの偏微分方程式は以下の形で表される方程式です。
$$\boldsymbol{P}(x,y,u)\frac{\partial u}{\partial x}+\boldsymbol{Q}(x,y,u)\frac{\partial u}{\partial y}=\boldsymbol{R}(x,y,u)\cdots①$$
本記事ではこの方程式の特性方程式を利用した一般解の求め方と特性方程式のグラフにおける意味を解説します。
特性方程式の導出
滑らかな曲面である関数\(u=(x,y)\)について\(x,y\)が媒介変数\(t\)で表されるとすると、全微分\(du\)は
$$\frac{du}{dt}=\frac{\partial u}{\partial x}\frac{dx}{dt}+\frac{\partial u}{\partial y}\frac{dy}{dt}\cdots②$$
ゆえに式①と式②は同じ形をしているから、式②は式①の両辺に任意定数\(k\)をかけたものであると言え、
$$kP=\frac{dx}{dt},kQ=\frac{dy}{dt},kR=\frac{du}{dt}\cdots③$$
が成り立ちます。
ゆえに式③を解けば関数\(u(x,y)\)を求めることができ、式③を特性方程式とよぶのです。
特性方程式
特性方程式は以下のように表せます。
$$kP=\frac{dx}{dt},kQ=\frac{dy}{dt},kR=\frac{du}{dt}$$
またはこの形から\(kdt\)を消去して以下のように書くこともできます。
$$\frac{dx}{P}=\frac{dy}{Q}=\frac{du}{R}$$
例題
以下の偏微分方程式を解け
$$yu\frac{\partial u}{\partial x}-xu\frac{\partial u}{\partial y}=xy$$
解答
この偏微分方程式の特性方程式は、
$$\frac{dx}{yu}=\frac{dy}{xu}=\frac{du}{xy}$$
(1)\(\frac{dx}{yu}=\frac{dy}{xu}\)について
変形すると、
$$xdx+ydy=0$$
両辺を積分すると、
$$\frac{x^2}{2}+\frac{y^2}{2}=\frac{C_1}{2}$$
ゆえに、$$x^2+y^2=C_1\cdots①$$
(2)\(\frac{dy}{xu}=\frac{du}{xy}\)について
変形すると、$$ydy-udu=0$$
ゆえに、$$x^2-u^2=C_2\cdots②$$
式①、②から2つの任意定数の間に\(\varphi(C_1,C_2)=0\)の関係が存在するとして、一般解は、
$$\varphi(x^2+y^2,x^2-u^2)=0$$
解曲面\(u(x,y)\)と特性方程式のグラフにおける意味
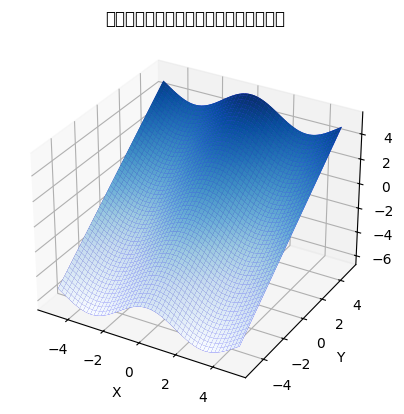
関数\(u=u(x,y)\)は\(xyu\)直交座標において左図のような滑らかな直線を表します。
この曲面を解曲面と呼び、接平面上の微小ベクトルは偏微分の定義から、
$$d\boldsymbol{a}=[dx,0,u_xdx],d\boldsymbol{b}=[0,dy,u_ydy]$$
ゆえに接平面上の1次独立な接線ベクトルは、
$$\boldsymbol{a}=[1,0,u_x],\boldsymbol{b}=[0,1,u_y]$$
となります。
このことから解曲面の接平面の法線ベクトル\(h\)は、
$$\boldsymbol{h}=\boldsymbol{a}\times\boldsymbol{b}=\begin{vmatrix}i & j & k \\ 1 & 0 & u_x \\ 0 & 1 & u_y \end{vmatrix}=[-u_x,-u_y,1]$$
ここでラグランジュの偏微分方程式を書き換えると、
$$-Pu_x+Qu_y+1=0\cdots④$$
ゆえに\(\boldsymbol{d}=[P,Q,R]\)とすると式④は、
$$\boldsymbol{h}\cdot\boldsymbol{d}=0$$
と変形することができます。この式から\(\boldsymbol{d}\)は法線ベクトル\(\boldsymbol{h}\)と垂直となり、\(\boldsymbol{b}\)は曲面の接平面上のベクトルであると言えます。
よって媒介変数\(t\)および任意定数\(k\)を用いて、
$$k[P,Q,R]=\left[\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}\right]$$
となり、このことからも特性方程式
$$kP=\frac{dx}{dt},kQ=\frac{dy}{dt},kR=\frac{du}{dt}$$
または
$$\frac{dx}{P}=\frac{dy}{Q}=\frac{du}{R}$$
を導出することができます。
ここで重要なのは特性方程式が導けたことに加えて解法から特性方程式の正体が見えてくるということです。
ベクトル\(\boldsymbol{d}\)は解曲線の接線ベクトルを表し、その接線ベクトルの軌跡となる特性曲線が特性方程式となります。
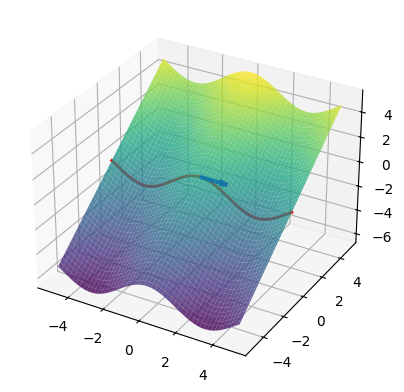
ある初期値\((x(t),y(t),u(t))\)を与えられた場合の特性方程式が左図の赤線となり、青の矢印が接線ベクトルとなります。
そのため異なる初期値での特性曲線が集まって解曲面になります。



コメント