本記事では熱力学第1法則や第2法則を学習するための準備として熱力学が観察の対象とする系とは何か、熱平衡状態とは、熱力学で登場する重要な変数である状態量とは何か、気体の状態を表す状態方程式について解説していきます。
系とはなにか
物理学において複数の物体をひとつにまとめた巨視的にひろがりをもつもの(気体など)を系と呼びます。
つまり、熱力学では観察する対象は物体そのものではなく系になります。
また、全体の一部分であり力接観察する系以外の部分を外界と呼び、系についても主に開放系、閉鎖系、断熱系、孤立系に分類されます。
開放系とは
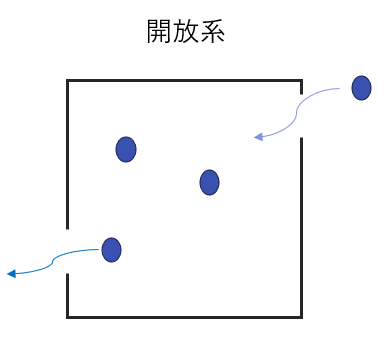
開放系とは左図のような物質の出入りがある系のことは指し、気体においては分子の数、つまり物質量が変化します。
逆に物質の出入りがない系のことを閉鎖系と呼びます。
断熱系と孤立系
断熱系とは熱の出入りがない系のことを指し、熱や仕事の出入りおよび物質の出入りがない系のことを孤立系と呼びます。
状態量と熱平衡状態
ある系とそれに作用する系に仕事や熱を与えず放置した場合、最初にどんなに乱雑な状態にあったとしても最終的にはほとんど変化のない状態へと落ち着きます。
このような状態のことを熱平衡状態とよびます。
この熱平衡状態において系は温度T、体積V、圧力P、分子数Nなどの少ないマクロ変数で表現することができ、このマクロ変数のことを状態量とよびます。
示量変数と示強変数
このとき状態量は示量変数と示強変数に分類され、
示量変数とは、系の大きさをx倍したときに同様にx倍される変数のことを指します。
状態量のなかで示量変数となるのは相加性をもつ体積Vと物質量Nです。
示強変数とは、系の大きさを変えても変化しない変数のことを指し、温度Tや圧力Pがこれに該当します。
系の状態を変数で表現するとき、(T;P,V)などのように(示強変数;示量変数)というように表記することがあります。
状態方程式と理想気体
\(\)状態量T,P,V,Nはそれぞれがすべて独立変数となるのではなく、\(f(T,P;V,N)=0\)のような関係が存在します。この式のことを状態方程式とよびます。
理想気体
nモルからなる気体の状態方程式について、以下の式がなりたつときその気体を理想気体とよびます。
$$PV=nRT$$
この式は\(P,V\)が反比例、\(P,T\)および\(V,T\)が比例する関係(ボイル・シャルルの法則)から導かれた式であり、分子間相互作用や分子の体積などのミクロな影響を考慮しないため理想気体の状態方程式と呼びます。
そのため分子間相互作用や分子の体積などのミクロな影響は高温または低圧になるほど無視でき理想気体に近づきます。
\(R\)は気体定数を指し、\(R=8.135 J\cdot mol^{-1}K^{-1}\)の値を取ります。



コメント