\(\)熱力学第1法則が\(dU=d’W+d’Q\)であることはすでに前の記事で述べました。この熱力学第1法則を利用して熱平衡状態の変化を計算するためには気体がどのように仕事するか、または仕事されるかを理解する必要があります。
本記事では様々な操作によって気体がどのように仕事をするか(されるか)、つまり\(W\)が具体的にどのように計算されるかを解説します。
気体の膨張による仕事
以下のようにシリンジの中の気体が外圧により生じる力に逆らって気体が膨張する場合を考えます。

気体が外圧による力\(F\)に逆らって距離\(dz\)だけ動かしたため気体がする仕事\(dW_{do}\)は
$$dW_{do}=Fdz$$
で表されます。そのため気体がされる仕事\(dW\)は\(dW=-dW_{do}\)より、
$$dW=-Fdz$$
外力が\(P_{ex}\)によるピストンの断面(断面積A)を押す力\(F\)は、
$$F=AP_{ex}$$
であるから、気体がされる仕事は\(Adz=dV\)であることを利用して、
$$dW=-AP_{ex}dz=-P_{ex}dV\cdots①$$
と表される。
ゆえに体積が\(V_i\)から\(V_f\)まで膨張するときのされる仕事\(W\)は両辺を積分すればよいから、
$$W=-\int_{V_i}^{V_f}P_{ex}dV\cdots②$$
式②が気体の膨張によりされる仕事になります。
ではさらに具体的に膨張の種類によって仕事がどのような値をとるか見てみましょう。
外圧が一定で気体が膨張する場合
シリンジの気体が常に一定な外圧\(P_ex\)に逆らって膨張する場合、式②は以下のように変形できます。
$$\begin{eqnarray}W &=& -\int_{V_i}^{V_f}P_{ex}dV \\ &=& -P_{ex}\int_{V_i}^{V_f}dV=-P_{ex}(V_f-V_i)\end{eqnarray}$$
ゆえに\(\Delta V=V_i-V_f\)であるから気体のされる仕事は、
$$W=-P{ex}\Delta V$$
で表されます。
可逆膨張する場合
可逆膨張とはシリンジ内の気体と外界の空気が可逆変化することでシリンジ内の気体が膨張することを意味します。
可逆変化とは無限小の変化に対して方向を逆転できる変化のことを指します。
つまり可逆変化で膨張した気体は膨張した時と逆の過程をたどれば元の状態に戻ることができます。
ここでシリンジで気体が可逆変化しながら膨張するには、以下のように外圧とシリンジ内の圧力が釣り合っている必要があります。
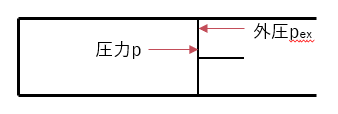
圧力と外圧が等しくない場合、摩擦力などの非保存力の働きにより逆の過程をたどっても元に戻らないからです。
ゆえに、可逆変化において
$$P=P_{ex}$$
が成り立つから、気体のされる仕事は
$$W=-\int_{V_i}^{V_f}PdV\cdots③$$
で表されます。
完全気体の等温可逆膨張
完全気体が等温可逆膨張するときの気体のされる仕事は、
\(P=nRT/V\)かつ式③から
$$W=-nRT\int_{V_i}^{V_f}\frac{dV}{V}=-nRT In{\frac{V_f}{V_i}}$$
となります。



コメント