自然界において熱は高温の物体から低温の物体に流れ、気体は温度が高くなり膨張したりなど自発的に変化する方向が決まっています。こうした現象を法則として表したものが熱力学第二法則であり、今回導入するエントロピーを用いて熱力学第二法則を表すことで自発変化がどの向きか、変化が可逆変化であるか不可逆変化であるかなどが計算でわかるようになります。本記事ではエントロピーと熱力学第二法則について詳しく解説していきます。
エントロピーとは
\(\)
先ほど述べたように自然界では高温の物体から低温の物体へ熱が流れ、また系が受け取った熱をすべて仕事に変えることはできません。
こうした法則のことを熱力学第二法則とよび、熱力学第二法則を式として表すためには新たにエントロピー\(S\)という状態量を導入する必要があります。
エントロピーの定義
エントロピー\(S\)について順静的過程において以下の等式が成り立ちます。
$$dS=\frac{d’Q}{dT}$$
このエントロピー\(S\)を用いることで熱力学第二法則を数式で表すことができるようになるのです。
定義だけではエントロピーが何かわからないためエントロピーが何を表すか説明します。
エントロピーの意味
エントロピーがなんであるかを言葉で表すとすれば乱雑さです。
微少量\(dS\)に関して言えば元の状態に比べ系がどれくらい乱雑になったかを表しているのです。
気体をミクロな視点でみれば、たくさんの粒子が飛び回っている状態になっているでしょう。
もし熱が\(d’Q\)加わればより粒子の持つエネルギーが大きくなり飛び回る速度が増加し、粒子同士がぶつかる回数も増え、より状態が乱雑に(複雑に)なります。
そのためエントロピーの微少量\(dS\)は\(d’Q\)に比例しているのです。
ですが高温な気体に熱が加わるのに比べて低温な気体に熱が加わるほうがより乱雑になると考えられます。高温な気体はすでに粒子が速い速度で運動している状態にあるからです。
ですから、それぞれ違う乱雑さである状態同士を比較するために熱量\(d’Q\)を温度\(T\)で割っています。
これがエントロピー\(S\)の正体になります。エントロピーの意味が分かれば熱力学第二法則をエントロピーで表した式についても簡単に理解できるでしょう。
熱力学第二法則(エントロピー増大則)
まずは系をミクロな視点で見てみましょう。
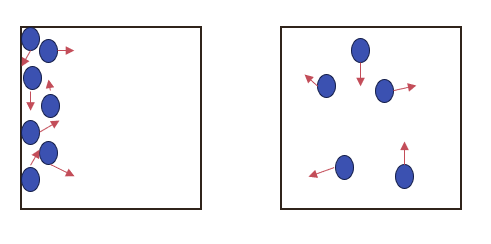
図のような孤立系内の粒子を考えます。
もし系の粒子が左図のような一部分に偏って存在している場合、粒子はさまざまな方向に運動していることから次の瞬間には右図のような粒子が系全体に分散した状態になっているでしょう。
このように外界から仕事や熱などが加わらない状態において系はより乱雑な状態になる方向へ変化します。これがミクロな視点で見た熱力学第二法則の解釈であり、エントロピーを用いて熱力学第二法則は以下のように記述されます。
熱力学第二法則(エントロピー増大則)
任意の断熱過程に対して常に\(\Delta S\geq 0\)が成り立つ。
つまり熱が加わらない断熱過程において系のエントロピーは常に増大していく方向に変化していくのです。
\(\Delta S=0\)が成り立つときが準静的過程であり、不可逆変化に関しては\(\Delta S \gt 0\)となります。
これが熱力学第二法則の正体になります。これを用いることで高温の系から低温の系へ熱が移動したりなどの自発変化の方向を知ることが可能になります。



コメント